本篇文章主要介绍了 Groth16 算法相关的基本概念、密码学基础和主要算法流程，以及重点展示了三种 Groth16 算法延展性攻击的攻击向量构造方法。

撰文：Saya，Beosin 安全研究专家

本篇文章依然是 Beosin 带给大家的硬核安全研究系列文章，今天我们来为大家讲解什么是 Groth16 证明延展性攻击。

1. 什么是延展性攻击？

2014 年 MT.GOX 交易所安全事件（也被称为「门头沟事件」），遭受了比特币上的交易延展性攻击 (Transaction malleability attack)，造成了约 85 万枚比特币的损失。此次攻击的具体过程如下：攻击者首先在 MT.GOX 发起一笔提现交易 A，接着在交易 A 被确认之前通过篡改交易签名，使得标识一笔交易唯一性的交易哈希发生改变，生成伪造的交易 B。

如果交易 B 比 A 先被矿工打包记录到比特币账本中，那么后续矿工在打包交易 A 的时候会因为 B 已经使用了同样的 UTXO 而认为 A 存在双花问题，从而拒绝打包 A。最后，攻击者向交易所申诉未收到代币，交易所会根据交易 A 去链上查询交易状态，发现提现交易确实未成功后会再次向攻击者转账，造成交易所资金流失。这种延展性攻击并未改变交易内容本身，而仅仅是改变了交易签名。

比特币的延展性攻击是椭圆曲线 ECDSA 签名算法存在的漏洞，比特币通过校验交易 id 是否已经存在，防止由于交易重放导致的双花攻击。而交易 id 是由交易内容的哈希自动生成，所以如果交易签名 sigscript 改变，则交易 id 也会随之改变，因此攻击者通过反转签名中的 S 值之后，可以伪造出另一个合法签名。但是这种攻击方式，无法改变交易的输入和输出。比特币在 BIP-141 中提出了隔离见证这一方案，通过将交易签名存储在 witness 中，不再置于交易数据中，可以防范该攻击并达到扩容的目的。

这种由于算法设计本身造成的延展性安全问题，在 zk 算法 Groth16 中同样存在，今天我们将为大家详细介绍 Groth16 证明延展性攻击。

2. Groth16 算法

Groth16 算法是使用最广泛的 zk-SNARKs(Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) 的非交互式零知识证明方案之一。相比于其他的 zk-SNARKs 算法，其生成的证明尺寸更小，验证速度更快，因此被应用到如 Zcash、celo 等项目中。下图列举了常见的 zk 算法：

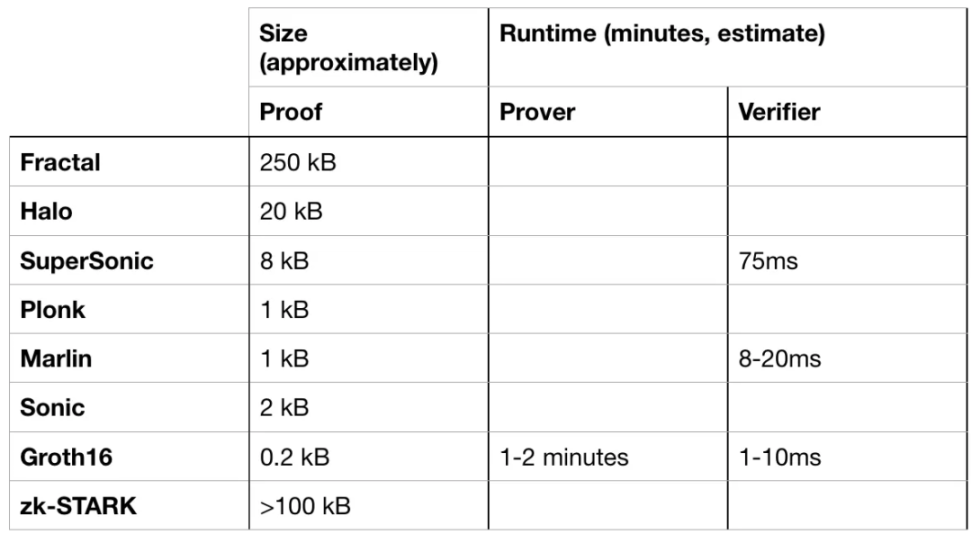
https://medium.com/coinmonks/comparing-general-purpose-zk-snarks-51ce124c60bd

2.1 Groth16 算法概述

通常一个 zk-SNARKs 零知识证明的 DApp 开发过程分为以下几个步骤，首先项目方会将业务逻辑抽象生成数学表达式，接着将其转化为 R1CS 描述的电路。

但是由于 R1CS 只能依次验证电路中的各个逻辑门，这种做法非常低效，所以 zk-SNARKs 算法将其转化为 QAP 电路，也就是将 R1CS 中用向量表示的约束转换为插值多项式，再生成可以在链下密码库或者链上合约中验证的证明，最后根据电路生成的验证合约将对生成的证明进行合法性校验。

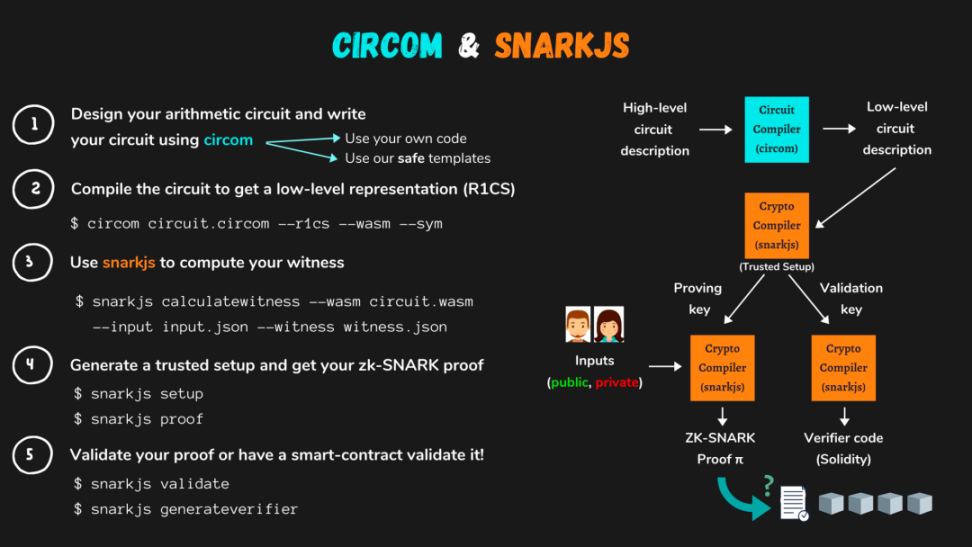
https://docs.circom.io/

其中，Groth16 算法作为一种 zk-SNARKs 算法，同样涉及到零知识证明电路，其二次算术电路的约束关系为：

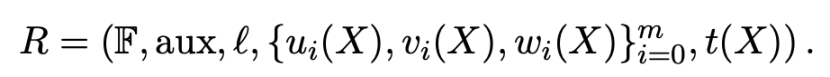
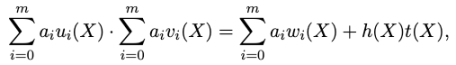
Groth16 算法就是为了证明 Prover 知道一组多项式的解 witness 即 h(x) 满足上式。

2.2 可信设置

由于 Groth16 算法在椭圆曲线域上进行计算，域上的值是一个个坐标点，那么如何使用坐标点表示多项式呢？这就需要使用椭圆曲线配对。关于椭圆曲线配对这里简单介绍一个例子，更为具体的解释请参考 V 神的博客: https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627。

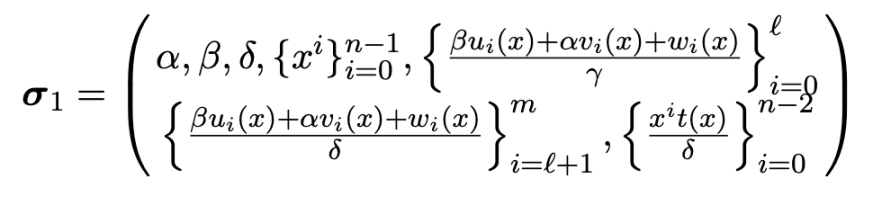
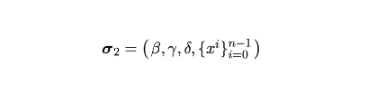
2.3 Prover 生成证明

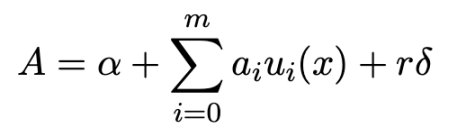
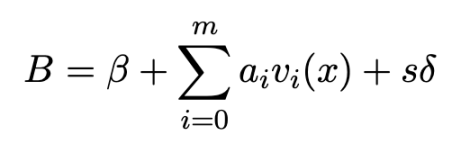
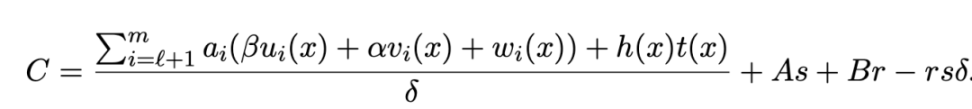
生成的证明如下图所示：

2.4 Ver­i­fier 验证证明

根据 Groth16 中使用的双线性配对，Verifier 接收到证明π[A、B、C]后验证如下方程：

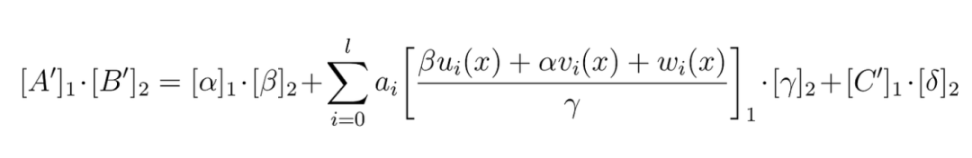
如果等式成立，则代表证明验证成功。

实际的项目验证过程中，还有第三个参数 public_inputs，该参数是电路的一组输入称为 statement，因为 Prover 和 Verifier 需要对计算和验证的证明有一个数据共识，即针对哪一组实际的数据生成证明并验证。

3. Groth16 算法延展性攻击

由于验证方程只要左右两式相等即可通过校验，则可将证明中的 A、B、C 伪造为 A‘、B’、C‘：

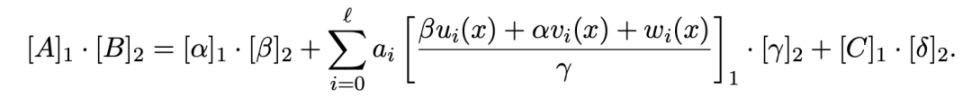
3.1 乘法逆元构造法

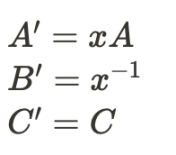
由于在有限域上进行计算，所以满足交换律和结合律，具体的推导过程如下：

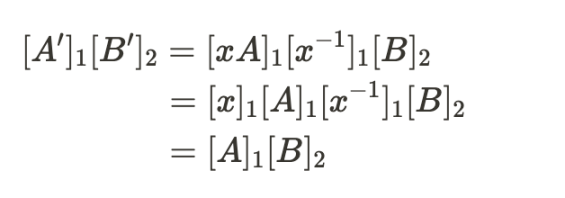
3.2 加法构造法

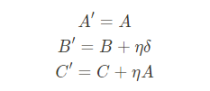
具体的推导过程如下：

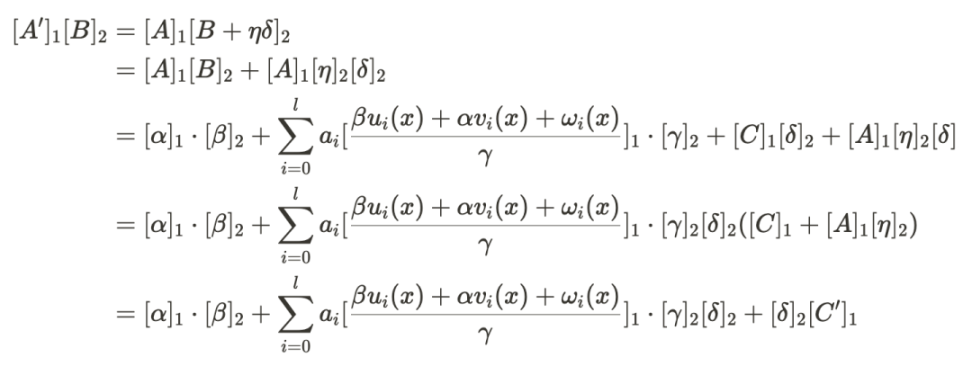
3.3 合并构造法

上述两种伪造证明的构造方式可以合并为下列表示式：

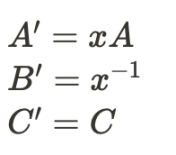
在 ark 代码库中已经有对应实现：

/// Given a Groth16 proof, returns a fresh proof of the same statement. For a proof π of a

/// statement S, the output of the non-deterministic procedure `rerandomize_proof(π)` is

/// statistically indistinguishable from a fresh honest proof of S. For more info, see theorem 3 of

/// [\[BKSV20\]](https://eprint.iacr.org/2020/811)

pub fn rerandomize_proof(

vk: &VerifyingKey<E>,

proof: &Proof<E>,

rng: &mut impl Rng,

) -> Proof<E> {

// These are our rerandomization factors. They must be nonzero and uniformly sampled.

let (mut r1, mut r2) = (E::ScalarField::zero(), E::ScalarField::zero());

while r1.is_zero() || r2.is_zero() {

r1 = E::ScalarField::rand(rng);

r2 = E::ScalarField::rand(rng);

}

// See figure 1 in the paper referenced above:

// A' = (1/r₁)A

// B' = r₁B + r₁r₂δ

// C' = C + r₂A

// We can unwrap() this because r₁ is guaranteed to be nonzero

let new_a = proof.a.mul(r1.inverse().unwrap());

let new_b = proof.b.mul(r1) + &vk.delta_g2.mul(r1 * &r2);

let new_c = proof.c + proof.a.mul(r2).into_affine();

Proof {

a: new_a.into_affine(),

b: new_b.into_affine(),

c: new_c.into_affine(),

}

}

4. 总结

本篇文章主要介绍了 Groth16 算法相关的基本概念、密码学基础和主要算法流程，以及重点展示了三种 Groth16 算法延展性攻击的攻击向量构造方法。

接下来的文章，我们将通过对 Groth16 算法常见的密码库实现攻击演示，来进一步展示验证性攻击。欢迎继续关注 Beosin 的后续文章。